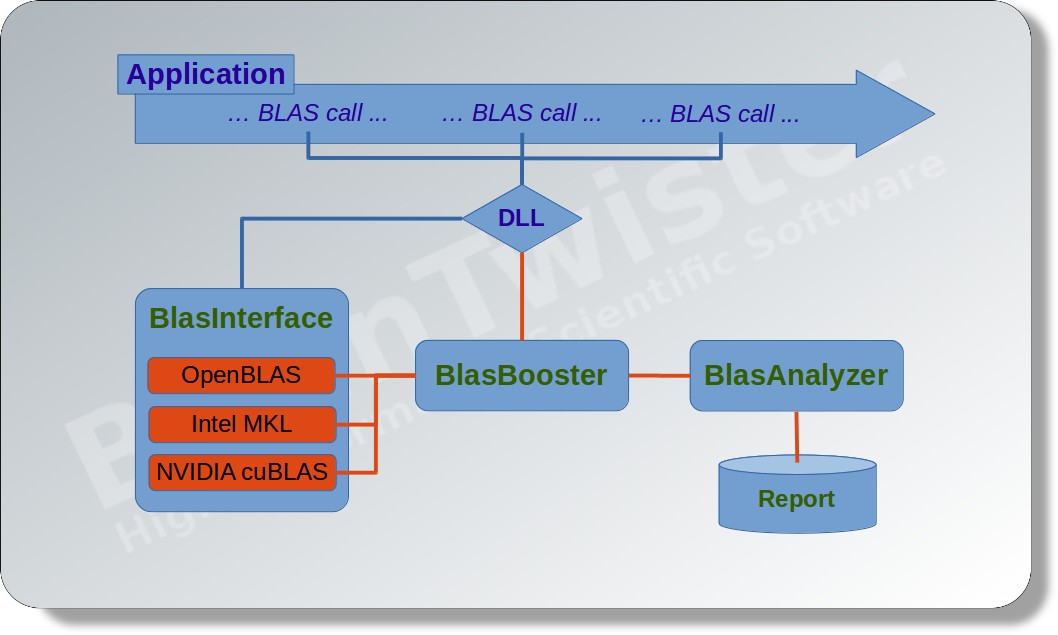
BlasBooster
Algorithms in the field of linear algebra are strictly separated into a dense and a sparse world. BlasBooster provides an opportunity to combine these two worlds in a dynamic way by dividing matrices and vectors with respect to their type, occupation and accuracy, so that in each case the most appropriate algorithm can by applied.
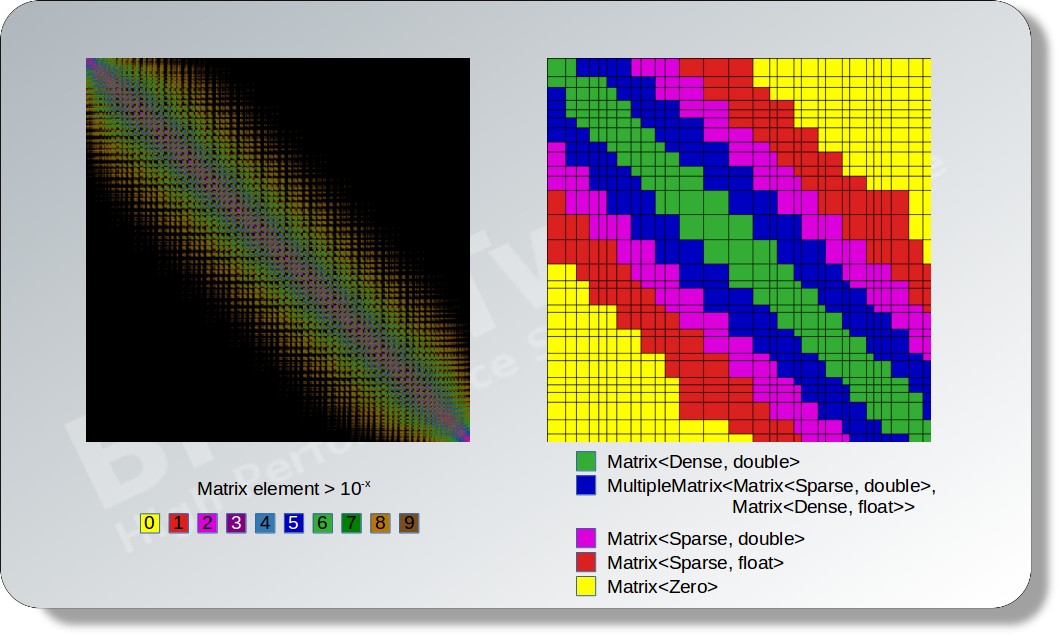
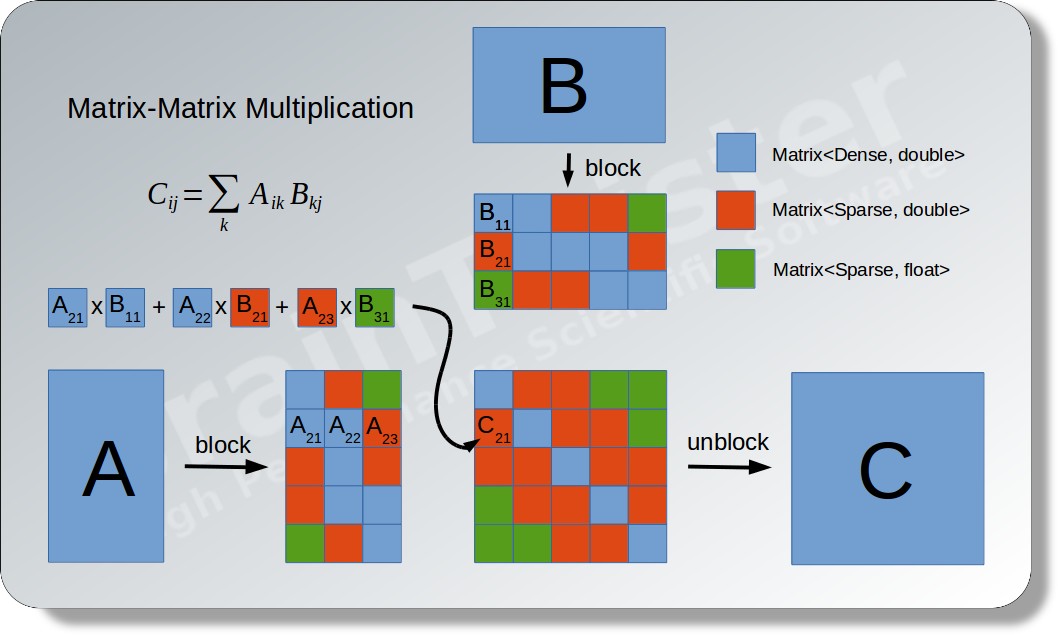
Let’s consider, for instance, a matrix-matrix multiplication. First, the matrices A and B will be divided into sub-matrices. Then, each sub-matrix will be converted into their ideal representation with respect to their occupation and significance. Typical matrix types are:
Matrix<Dense, double>Matrix<Dense, float>Matrix<Sparse, double>Matrix<Sparse, float>MultipleMatrix<Matrix<Sparse, double>, Matrix<Dense, float>>MultipleMatrix<Matrix<Sparse, double>, Matrix<Sparse, float>>
Here, the MultipleMatrix is a special, composed matrix type which is comparable to an expression template of a matrix sum. The type MultipleMatrix<Sparse, double>, Matrix<Dense, float>>, for instance, is useful if a matrix have many small entries which can be stored in single precision and only some entries which must be stored in double precision.
For the actual multiplication A x B, several multiplications of sub-matrices of different types will be performed and summed up to the the resulting matrix C.
In addition to the direct usage of the BlasBooster interface, the conventional BLAS standard is also supported. Therefore, it is possible to use BlasBooster without any changes within your application by only linking the BlasBooster library instead of the conventional BLAS library like OpenBLAS, IntelMKL, or NVIDIA cuBLAS. Moreover, the special module BlasAnalyzer assess your application with respect to the BLAS usage and reports a summary of all relevant values and timings.